Jun

11

One of the most common problems when studying markets is deciding whether to study levels, or the changes themselves. For example, when looking at weekly levels of stock market prices, one knows that the changes between the consecutive closes might not contain all the regularities, yet by analyzing the levels one runs into the problem of serial correlation, with levels near the previous being much more likely than the mean level.

In Data Analysis Tools # 11, which I found helpful in writing this piece, they list four reasons for such serial correlation:

  1. The market has a trend within the period. In the following case the levels at the beginning are closer together than the levels at the end of the period, which is what makes the serial correlation.
  2. The market varies seasonally, which has been overlooked. This would apply more to economic announcements, with the always suspect seasonality corrections.
  3. The market is missing some explanatory variables that are serially correlated, like bonds and the dollar.
  4. The market includes random noise that is serially correlated or that has persistent effect, (that being the name of the game of course).

The usual method of handling this problem is to take first differences, but this has several technical problems due to the implicit assumption one has to make as to the correlation between the consecutive levels and errors. There are several parametric solutions to this, but as far as practical market work goes, they induce so much data fitting and variability to the analysis. In my opinion they are merely window dressing for academic practitioners, whose purpose is to invent methods that are results impossible to duplicate by the layman, therefore maintaining the academics' ivory towers, useful for consulting and marketing purposes.

A solution that is often used for for problems of this nature is to take the ranks of the levels of changes and apply the normal methods of correlation on the ranks. Whilst going through the book Rank Correlation Methods, I wondered if the use of Tau as a correlation measure might unravel many of the statistical problems in testing for randomness in such a series. I reflected on such, and came across several papers that had taken similar technical approaches, including a Kendall's Tau for Autocorrelation by Ferguson et. al., in the Canadian Journal of Statistics.

The results and procedures of that paper are interesting, but I found it better to continue pursing the subject on my own, as I believe the methodology and approach I take is more direct and relevant to market analysis. Let us start with what Tau is, adopted from Kendall himself.

Suppose a number of boys are ranked according to their ability on mathematics and music:

BOY       A   B   C   D    E
Math      7   4   3   10   6
Music     5   7   3   10   1

Let us consider boys A and B; B is below A on math, but on music, B is above A — their ranks are in opposite order in this comparison. Now if we look at C, he is below A on math and below A on music, making it in natural order. D is above A in both subjects, so again this in natural order. E is also below A on both, so in natural order. Three of A's relationships were in natural order and one was not.

Let us now focus on boy B. He is in natural order with C, natural order with D and in opposite order with E. That is 2 in natural order in 1 out. Now C is in natural order with D and E. That is two more relationships in natural order. D is in Natural order with E, which is another relationship in natural order — thus of ten possible comparisons, there were eight in natural order, and two not.

Tau would be computed as six out of ten (the number concordant minus the number discordant), and it could have varied from plus one to minus one.

Now let us consider using Tau as a test for trend, where we look at time as one variable and price as the other. Here are prices starting with Friday January 5th and ending with Friday January 12th, this year.

DAY          NATURAL     LEVEL
Fri, 05,        1             1442.3
Mon, 08      2             1448.5
Tue, 09       3             1446.7
Wed, 10      4             1450.6
Thur, 11      5             1457.6
Fri, 12         6             1467.6

There are fifteen possible comparisons here, and of these fifteen, only one is discordant, (out of natural order) — Tuesday with Wednesday, with Wednesday being down from Tuesday, but coming later in the week. Thus there were 14 in natural order, and tau for the week would be 13/15 = 0.87.

I believe that the absolute value of Tau computed in such a manner for each week, with positive Tao meaning a positive trend and vice versa, is a good measure of the trendiness in the market for the week. Here are Tau calculations for the first few weeks of the year, and then last week, for S&P futures.

Week Ending   Tau measure of Trend.
Jan 05                -0.6
Jan 12                0.90
Jan 19                -0.6
Jan  26               -0.2
Feb 02                 0.9
Feb 09                0.07
Feb 16                0.7
Feb 23               -0.60
Jun 08               -0.7

The tendencies are apparent even in this cursory analysis, which will doubtless be finalized by the young intern scion, and compared with the random character of the actual price changes in the series, by the artful simulator, Mr. Tom Downing.

Steve Ellison adds: 

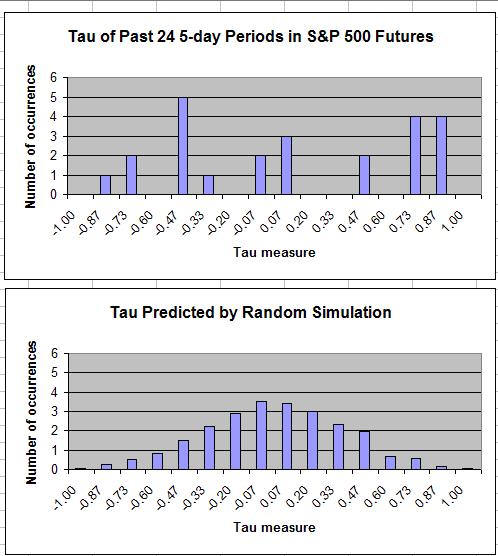
I generated 2400 random sequences of 6 numbers and calculated the tau measures of each sequence. I then calculated the tau measure for each of the past 24 5-day periods in the S&P 500 futures. The distribution of the S&P 500 tau measures appears quite different from the randomly generated distribution.


Comments

Name

Email

Website

Speak your mind

Archives

Resources & Links

Search