|
|
|
|
 |
Daily Speculations The Web Site of Victor Niederhoffer & Laurel Kenner Dedicated to the scientific method, free markets, deflating ballyhoo, creating value, and laughter; a forum for us to use our meager abilities to make the world of specinvestments a better place. |
Write to us at:
 (address is not clickable)
(address is not clickable)
06/28/2004
The Tower of
Hanoi
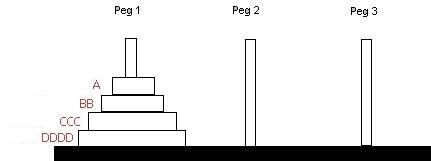
Let's say you have four horseshoes of different size and three pegs with the horseshoes all stacked on the leftmost peg so that the biggest one is at the bottom, the second biggest one is on top of that, and the third biggest is on top of that, and the smallest is at the very top.
The problem is to move the horseshoes to Peg 3 one by one without ever putting a bigger horseshoe on top of a smaller horseshoe. In other words the moves must be such that the smaller horseshoe is never below a bigger one on a peg.
How many moves does it take to accomplish the task?
if you simplify the problem so that there are two pegs A and BB BB on Peg 1. you can see by trial and error it takes three moves. if you have three pegs it will take seven moves. and one peg takes one move.
Indeed, to move four pegs will take 24 -1 moves., i.e. 15 moves.
Books on difference equations show how to solve this problem. (Best one: An Introduction to Difference Equations by Saber Elaydi) The idea is that to accomplish the task you need to leave the biggest horseshoe DDDD on peg 1 and move the three other horseshoes to the second peg with the second-biggest, CCC, at the bottom, BB on top of that , and then A at the very top.
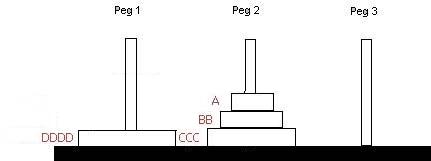
In other words an intermediate step is to leave the biggest one alone and then put the other three onto Peg 2 in the order they started with with the biggest on the bottom.
Step back to the situation with only three horseshoes on Peg 1 to start with where you can move them onto Peg 3 in seven moves. It will take you seven additional moves to move the horseshoes A, BB, and CCC from Peg 1 to Peg 2 so that you have them in order. The final step begins with moving DDDD to Peg 3. Thus, the problem is solved in stages with the number of moves to get into each stage the same as the number of moves to get to the next stage equal to the number of moves to get into the previous stage + 1 .
This is a difference equation of the form
n(t+1)= n(t) + n(t) + 1. with
n(1)=1. n(2) = 1 + 1 + 1. =3
n(3) = 3 + 3 +1. = 7
and n(t) = 2t like 24 , = 16
less the one.
I hypothesize that markets must go through similar intermediate stage for a consonance to occur. First one market goes to the top, then another, until an ultimate harmony occurs.
For example, bonds must go up the most first, more than the stock market. Then gold must follow, going up the most. Finally it is the stock market's turn to move to the fore. Such is happening today. with bonds up the beginning of last week, and then gold up the end of last week, (through the terrible round), and now the stocks opening up a google today.
The problem may be generalized to the rotation of industries within a given market, or perhaps the rotation of commodities like soybeans, corn, rye ,barley and wheat within the grains.
Such are the thoughts engendered by having six Montessori children and wishing to play with them on yet another level where they can beat their dad.