Daily Speculations
|
|
|
|
Daily Speculations |

Write to us at:
![]() (address is not clickable)
(address is not clickable)
The Sun-Baked Speculator
Tom Ryan
10/5/2005
Polar Coordinates, Revisited
I routinely use polar coordinates in my work and would be remiss if I did not comment on this subject. Polar coordinates are very useful for visualization of data where you have three to four dimensions. For example, while in Montana several weeks ago, I conducted mapping to determine the three dimensional geometry of a vein of ore cut by several faults. (fig. 1) By using polar coordinates, and a compass, one can quickly measure the attitude of the vein using two measures; the strike of the vein which is the angular measurement from the north pole of the line that the vein makes when crossing the horizontal plane, and the dip of the vein which is the measurement of the angle between the vein and the horizontal plane in a direction that is orthogonal to the line of strike. These two angular measurements are all that is needed to describe the three dimensional planar body in a polar coordinate system. Similarly, two angular measurements can be used to describe a line in three dimensional space (trend angle and plunge angle) by projecting the line onto the horizontal plane. In this case it was obvious even with just a few measurements that the faults were indeed changing the orientation of the vein from block to block and therefore this needed to be taken into consideration of any projection of where the vein was going.
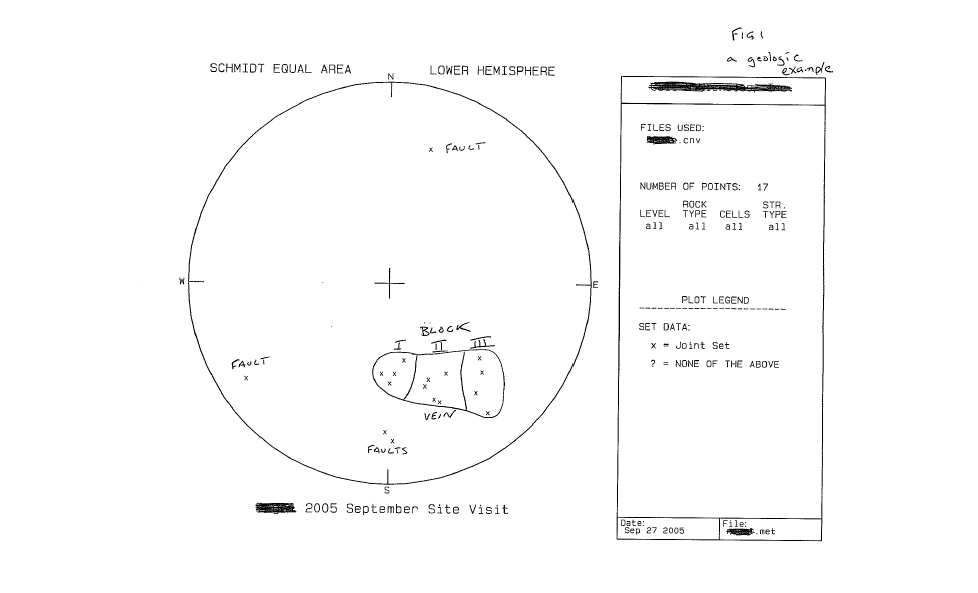
So the first advantage of the polar coordinate system is that it facilitates the measurement of complex geometries. The second advantage of using polar coordinates in any geometric problem, is that it is far easier to visually analyze geometrical variance when using polar coordinates rather than tables of numerical values. Converting x-y-z data to a polar coordinate system and plotting the data in the hemispherical projection does not change the data, however it does change the spatial relationships between the individual data points. Finally, using polar coordinates helps with geometric projections, and the analysis or understanding of geometric relationships, such as intersections of geometric bodies.
For visualizing data, there are two common hemispherical projection methods for projecting the 3-d sphere to a plane; the first utilizes equal angles (Wulff net), the second uses equal areas (Schmidt net). The underlying math for each construction can be Googled so I won't go into the math used for the two types of projections. Equal angle projections are used to analyze geometric interactions (such as finding the three dimensional orientation of the intersection of two planes), while equal area projections of three dimensional space are more commonly used for statistical analysis of many measured features (such as fault planes in rock).
For an example of how this might work with non-geologic data I took the daily change for the S&P500 in 2005, the daily change in the 10 year bond in 2005, and the daily change in Newmont Mining common stock, one of the larger publicly traded gold mining stocks. By assigning the change in the S&P to the x axis, the change in the bond to the y axis and the change in NEM common to the z axis, I can use the three daily change numbers to calculate a vector in 3-dimensional space for each trading day, similar to what Dr. Castaldo was doing. These can be converted to two angles for plotting in a polar coordinate system, the trend varying from 0-360 degrees, with plunges of 0-90 degrees, and then the vectors can be easily plotted in the polar system using a Schmidt equal area projection where each vector, moving outward from the origin, is represented by its pierce point on the outer shell of the globe which is then projected to the horizontal plane (or any other plane of our choosing although the horizontal plane is the standard method). In this case I have segregated the data into two data sets, days when NEM is up and days when NEM is down. Each data point was then labeled with a symbol to denote whether the next day NEM was up, up more than 2%, down, or down more than 2%. Figure 2, 3 present the data generated and plotted in a polar coordinate system. To understand the relationships, consider the four quadrants (NE, SE, SW, NW). In this case because of my assumptions, the NE quadrant represents days when bonds are up and stocks are down, the SE quadrant represents days when bonds and stocks are both down, the SW quadrant represents days when stocks are up and bonds are down, and the NW quadrant represents days when stocks and bonds are both up. Furthermore, to confuse the reader, I have plotted orthogonal vectors rather than the vectors themselves, so that steeply plunging vectors lie on the outer edge of the circle and flatter vectors appear near the origin (small changes near the center, big changes are near the outer edge).
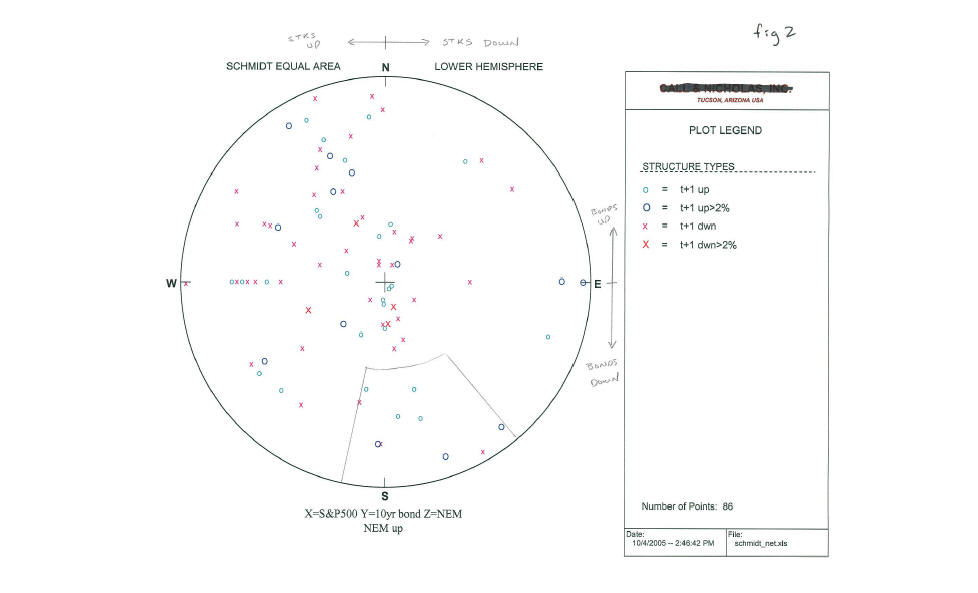
The first thing that is easily noted is that NEM and the S&P500 have a very positive correlation coefficient on up days for the market. That is when stocks are up, NEM is typically up (although not always). This can be seen by the absence of data points on the eastern half of chart 2 for up days in NEM. It is uncommon for NEM to be up when stocks are down. Other relationships can be seen. One of the more interesting is outlined on both figs 2 and 3 - the region in the southern part of the chart when stocks are up slightly to down moderately, and bonds are down more than stocks. When NEM has been up on such days, 7 out of the next ten trading days NEM has been up again including several big up days of greater than 2%. Even more interestingly, on days when bonds are down sharply and stocks are up slightly to down moderately, and NEM is also down, it is similarly bullish (for exact same region on the chart) the next day with 11 of 14 up at t+1.
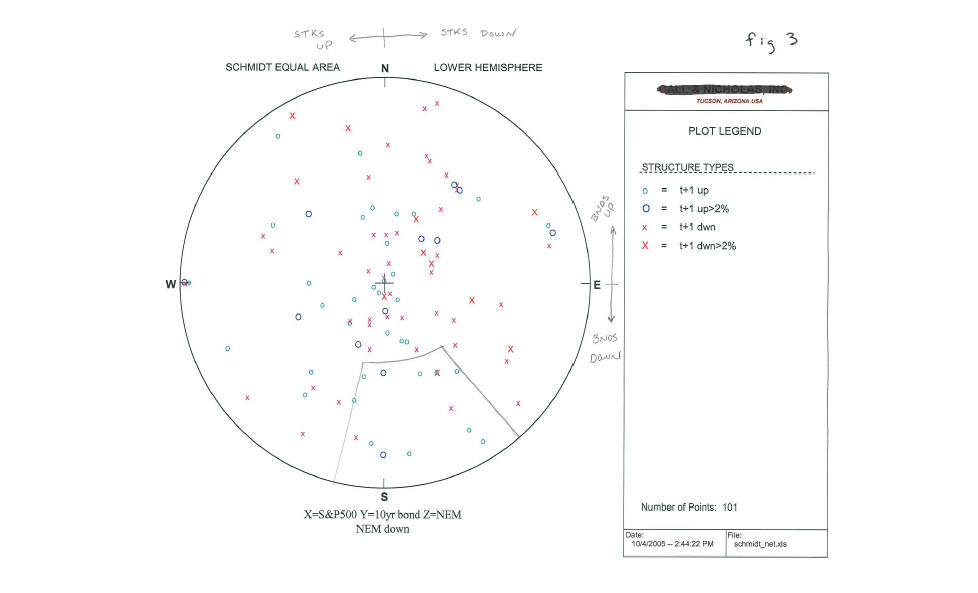
These are small samples and would need to be tested further by enterprising traders, but are used for illustration purposes as to how one might use a polar coordinate transform to analyze stocks or market interrelationships and from this one might conclude that gold stocks are worth a look for a trade whenever the s&p is up slightly or down moderately and bonds are down more than stocks. That is, in 2005, there appears to have been a tendency for money to rotate into gold whenever stocks are weak and bonds have had a particularly rough day at the office.